报告名称:The 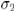 -curvature equation on a compact manifold with boundary
-curvature equation on a compact manifold with boundary
报告专家:韦韡
专家所在单位:南京大学
报告时间:2023年8月31日周四15:00-16:00
报告地点: 腾讯会议:474-437-376
专家简介: 韦韡,现南京大学研究员,博士毕业于中国科学技术大学,上海数学中心博士后。曾获得博士后创新人才计划。在 Adv.Math, J.Funct. Anal., Calc. Var.等杂志发表过多篇高质量论文。
报告摘要:We first establish local $C^2$ estimates of solutions to the $\sigma_2$-curvature equation with nonlinear Neumann boundary condition. Then, under assumption that the background metric has nonnegative mean curvature on totally non-umbilic boundary, for dimensions three and four we prove the existence of a conformal metric with a prescribed positive $\sigma_2$-curvature function and a prescribed nonnegative boundary mean curvature function. The local estimates play an important role in blow up analysis in the latter existence result.
